![Keadaan Industri Musik [PICS]](https://gadget-info.com/img/entertainment/673/state-music-industry.png)
Tidak seperti, standar deviasi adalah akar kuadrat dari nilai numerik yang diperoleh saat menghitung varians. Banyak orang membandingkan kedua konsep matematika ini. Jadi, artikel ini berupaya menjelaskan perbedaan penting antara varian dan standar deviasi.
Grafik perbandingan
| Dasar untuk Perbandingan | Perbedaan | Standar deviasi |
|---|---|---|
| Berarti | Varians adalah nilai numerik yang menggambarkan variabilitas pengamatan dari rata-rata aritmatika. | Deviasi standar adalah ukuran dispersi pengamatan dalam satu set data. |
| Apa itu? | Ini adalah rata-rata penyimpangan kuadrat. | Ini adalah akar kuadrat deviasi. |
| Diberi label sebagai | Sigma-kuadrat (σ ^ 2) | Sigma (σ) |
| Disajikan dalam | Unit kuadrat | Unit yang sama dengan nilai dalam set data. |
| Menunjukkan | Seberapa jauh individu dalam suatu kelompok tersebar. | Berapa banyak pengamatan dari set data berbeda dari rata-rata. |
Definisi Varians
Dalam statistik, varians didefinisikan sebagai ukuran variabilitas yang mewakili seberapa jauh anggota grup tersebar. Ini menemukan tingkat rata-rata di mana setiap pengamatan bervariasi dari rata-rata. Ketika varians dari set data kecil, itu menunjukkan kedekatan poin data dengan rata-rata sedangkan nilai varians yang lebih besar menyatakan bahwa pengamatan sangat tersebar di sekitar rata-rata aritmatika dan dari satu sama lain.
Untuk data yang tidak diklasifikasikan :
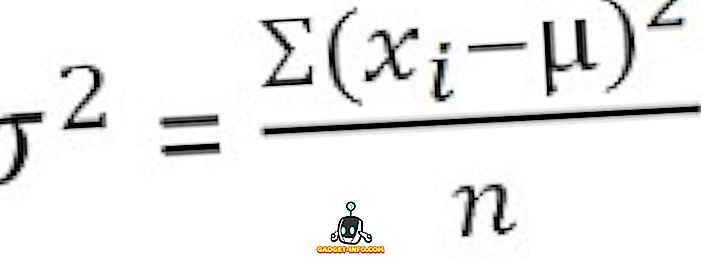
Untuk distribusi frekuensi yang dikelompokkan :
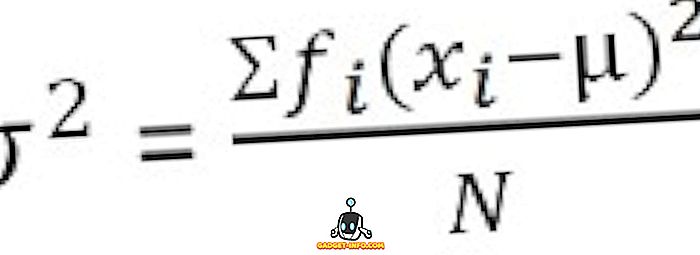
Definisi Standar Deviasi
Standar deviasi adalah ukuran yang mengukur jumlah dispersi pengamatan dalam dataset. Deviasi standar rendah adalah indikator kedekatan skor dengan rata-rata aritmatika dan deviasi standar tinggi mewakili; skor tersebar pada rentang nilai yang lebih tinggi.
Untuk data yang tidak diklasifikasikan :
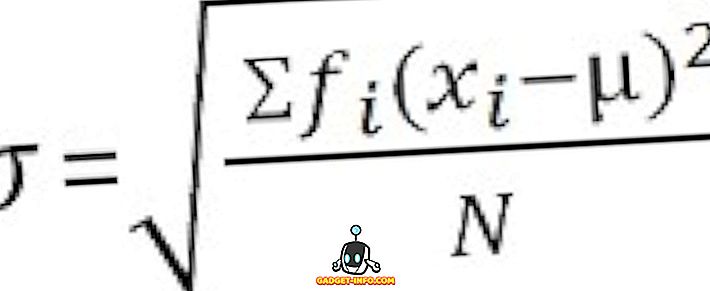
Perbedaan Kunci Antara Varians dan Standar Deviasi
Perbedaan antara deviasi standar dan varians dapat ditarik dengan jelas dengan alasan berikut:
- Varians adalah nilai numerik yang menggambarkan variabilitas pengamatan dari rata-rata aritmatika. Deviasi standar adalah ukuran dispersi pengamatan dalam satu set data.
- Varians hanyalah rata-rata penyimpangan kuadrat. Di sisi lain, simpangan baku adalah simpangan kuadrat rata-rata akar.
- Varians dilambangkan dengan sigma-squared (σ2) sedangkan standar deviasi dilabeli sebagai sigma (σ).
- Varians dinyatakan dalam satuan kuadrat yang biasanya lebih besar dari nilai dalam dataset yang diberikan. Berbeda dengan standar deviasi yang dinyatakan dalam unit yang sama dengan nilai-nilai dalam set data.
- Variance mengukur seberapa jauh individu dalam suatu kelompok tersebar. Sebaliknya, Deviasi Standar mengukur seberapa banyak pengamatan pada set data berbeda dari rata-rata.
Ilustrasi
Nilai yang dicetak oleh seorang siswa dalam lima mata pelajaran adalah 60, 75, 46, 58 dan 80 masing-masing. Anda harus mengetahui standar deviasi dan varians.
Pertama-tama, Anda harus mencari tahu artinya,
Jadi nilai rata-rata (rata-rata) adalah 63, 8
Sekarang hitung variansnya
| X | SEBUAH | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
Di mana, X = Pengamatan
A = Mean Aritmatika
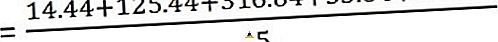
Dan standar deviasi adalah -
Kesamaan
- Baik varians dan standar deviasi selalu positif.
- Jika semua pengamatan dalam set data identik, maka standar deviasi dan varians akan menjadi nol.
Kesimpulan
Keduanya adalah istilah statistik dasar, yang memainkan peran penting dalam berbagai sektor. Deviasi standar lebih disukai daripada rata-rata karena dinyatakan dalam satuan yang sama dengan pengukuran sementara varians dinyatakan dalam satuan yang lebih besar dari kumpulan data yang diberikan.
