Berbeda dengan ini, dalam kasus kombinasi, urutan tidak masalah sama sekali. Tidak hanya dalam matematika tetapi dalam kehidupan praktis juga, kami menjalani kedua konsep ini secara teratur. Meskipun, kami tidak pernah memperhatikannya. Jadi, baca artikel itu dengan seksama, untuk mengetahui bagaimana kedua konsep ini berbeda.
Grafik perbandingan
| Dasar untuk Perbandingan | Permutasi | Kombinasi |
|---|---|---|
| Berarti | Permutasi mengacu pada berbagai cara mengatur satu set objek dalam urutan berurutan. | Kombinasi mengacu pada beberapa cara memilih item dari serangkaian besar objek, sehingga urutannya tidak menjadi masalah. |
| Memesan | Relevan | Tidak relevan |
| Melambangkan | Pengaturan | Pilihan |
| Apa itu? | Elemen yang dipesan | Set tidak terurut |
| Jawaban | Berapa banyak susunan berbeda yang dapat dibuat dari satu set objek tertentu? | Berapa banyak kelompok berbeda yang dapat dipilih dari kelompok objek yang lebih besar? |
| Penurunan | Permutasi ganda dari satu kombinasi. | Kombinasi tunggal dari permutasi tunggal. |
Definisi Permutasi
Kami mendefinisikan permutasi sebagai cara berbeda untuk mengatur beberapa atau semua anggota himpunan dalam urutan tertentu. Ini menyiratkan semua kemungkinan pengaturan atau penataan ulang set yang diberikan, ke dalam urutan yang dapat dibedakan.
Misalnya, Semua kemungkinan permutasi dibuat dengan huruf x, y, z -
- Dengan mengambil ketiganya sekaligus adalah xyz, xzy, yxz, yzx, zxy, zyx.
- Dengan mengambil dua sekaligus adalah xy, xz, yx, yz, zx, zy.
Total jumlah kemungkinan permutasi dari n hal, diambil r pada suatu waktu, dapat dihitung sebagai:
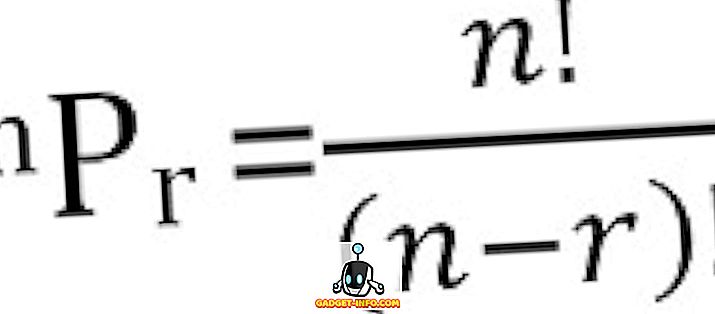
Definisi Kombinasi
Kombinasi tersebut didefinisikan sebagai cara berbeda, memilih grup, dengan mengambil beberapa atau semua anggota set, tanpa urutan berikut.
Misalnya, Semua kemungkinan kombinasi yang dipilih dengan huruf m, n, o -
- Ketika tiga dari tiga huruf harus dipilih, maka satu-satunya kombinasi adalah mno
- Ketika dua dari tiga huruf harus dipilih, maka kombinasi yang mungkin adalah mn, tidak, om.
Jumlah total kombinasi yang mungkin dari n hal, yang diambil r pada suatu waktu dapat dihitung sebagai:
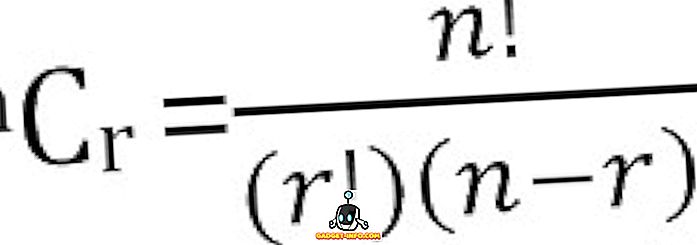
Perbedaan Kunci Antara Permutasi dan Kombinasi
Perbedaan antara permutasi dan kombinasi digambar dengan jelas berdasarkan alasan berikut:
- Istilah permutasi mengacu pada beberapa cara mengatur sekumpulan objek dalam urutan berurutan. Kombinasi menyiratkan beberapa cara memilih item dari kumpulan besar objek, sehingga urutannya tidak relevan.
- Titik pembeda utama antara dua konsep matematika ini adalah urutan, penempatan, dan posisi, yaitu dalam karakteristik permutasi yang disebutkan di atas tidak masalah, yang tidak masalah dalam kasus kombinasi.
- Permutasi menunjukkan beberapa cara untuk mengatur barang, orang, angka, huruf, warna, dll. Di sisi lain, kombinasi menunjukkan berbagai cara memilih item menu, makanan, pakaian, subjek, dll.
- Permutasi tidak lain adalah kombinasi yang diurutkan sementara Combination menyiratkan himpunan yang tidak teratur atau pasangan nilai dalam kriteria tertentu.
- Banyak permutasi dapat diturunkan dari satu kombinasi. Sebaliknya, hanya kombinasi tunggal yang dapat diperoleh dari permutasi tunggal.
- Jawaban permutasi Berapa banyak pengaturan berbeda yang dapat dibuat dari satu set objek tertentu? Berbeda dengan kombinasi yang menjelaskan Berapa banyak kelompok berbeda yang dapat diambil dari kelompok objek yang lebih besar?
Contoh
Misalkan, ada situasi di mana Anda harus mencari tahu jumlah total sampel yang mungkin dari dua dari tiga objek A, B, C. Dalam pertanyaan ini, pertama-tama, Anda perlu memahami, apakah pertanyaan itu terkait dengan permutasi atau kombinasi dan satu-satunya cara untuk mengetahui hal ini adalah dengan memeriksa apakah pesanan itu penting atau tidak.
Jika urutannya signifikan, maka pertanyaannya terkait dengan permutasi, dan sampel yang mungkin adalah, AB, BA, BC, CB, AC, CA. Di mana, AB berbeda dari BA, BC berbeda dari CB dan AC berbeda CA.
Jika urutannya tidak relevan, maka pertanyaannya terkait dengan kombinasi, dan sampel yang mungkin adalah AB, BC, dan CA.
Kesimpulan
Dengan diskusi di atas, jelas bahwa permutasi dan kombinasi adalah istilah yang berbeda, yang digunakan dalam matematika, statistik, penelitian, dan kehidupan kita sehari-hari. Satu hal yang perlu diingat, mengenai dua konsep ini adalah bahwa, untuk sekumpulan objek tertentu, permutasi akan selalu lebih tinggi daripada kombinasinya.